「生理反応重力場の理論」についての試論 ～Vol.３～

流れと渦

似た形や関係(構造)から類推するアナロジー思考は、直感的であり、論理の飛躍や誤謬に繋がることもあるが、直観的に事物の本質を捉えることも少なくない。
宇宙の創生を神々の働きへ擬人化したギリシア神話の構造は、現代の科学的宇宙論の創生説に非常に近いし、ピュタゴラスは宇宙を弦の振動数比のような数で出来ていると考えた。(現代物理の超弦理論に近い)
宇宙を流れと渦に捉える考え方にも古い歴史があり、古代ギリシアのヘラクレイトスの「万物流転」は熱力学の非平衡開放系の考え方に近いし、近代ではデカルトの「渦動説(近接作用説)」がある。デカルトの「ものに力が伝わるのには直接触れていないとならない(エーテルという架空伝達媒質の存在)」という考え方は、ニュートンの万物引力の「遠隔力」と対立するため、ニュートンは渦動説を批判したとされる。
しかし、相対論的重力が正しいのなら、むしろ見直されるべきはニュートンの遠隔力であり、時空間のひずみがつくる重力を伝達する媒質に求めるなら、現代宇宙論はエーテルに代わる媒質を探していることに他ならず、その意味においてデカルトのエーテル渦動説の焼き直しに過ぎず、媒質の名前がエーテルからグラビトンやヒッグス粒子に代わるだけなのではないだろうか。

構造医学創始者　吉田勧持先生は、川の流れを遡上するサケの姿に、重力に抗しながら応ずる生命の本質を捉えた。
重力は目に見えないが、物質の形へ化身し、その機能は自然の運動に「態の推移変化(流れ)」として表現されているのであり、見えない未知の物質を探すのもいいが、まず観える世界の現象をしっかりと観ることも大切ではないだろうか。
ここで言語概念の根本的意味に還ると、「力」とは自性せず、相互関係間の作用であること、また抵抗なきところに力なし、「暖簾に腕押し、糠に釘」が力の本質を表している。

アインシュタインへ相対性理論の着想を与えたのはマッハの原理だが、その言葉をひくと、「慣性力は宇宙の全質量の作用として考えなければならない」とし、回転するバケツの水面をへこませる慣性力について「慣性力はバケツが絶対空間に対してまわったから発生したのではなく、宇宙が回転するバケツに、ある作用を及ぼした結果、発生した」と続け、さらに「バケツがまわることと、バケツを止めて宇宙をバケツのまわりに逆回転させることは同等である」とする究極の相対論を展開した。 圧縮流体中における超音速気流の衝撃波(キャビテーション)の研究で業績を残しているマッハだけに、何もみえない空間にも波動伝達媒質が充満しているイメージがあったと思われ、そうでないとこのような発想転換は生まれないと思う。
筆者はこの言葉を知って、「パスカルの原理」を想起した。万有引力のような遠隔力ではなく、重力という時間的な見えない空間媒質を通じて宇宙という全体系内(容器内)での質量と運動が釣り合う姿はパスカルの原理そのものである。
重力と時間の流れを川の流れに例えれば、宇宙全体の本流の流れに対し、能動的に動く(固有の時間をもつ)もの、つまり枝分かれした支流の流れを本流に引き戻すようなものに思え、重力質量とは重力が一時的に「物質へと化身した仮の姿」であり、本質はその機能即ち慣性（流れ）抵抗にあると考える。
その重力の流れと物質運動の適切な関係を形成するものが「摩擦とその制御（潤滑）」であるから、構造医学の理論の最初に「生体潤滑理論（バイオトライボロジー）」が記されている意味が改めて理解できるのである。また流体中移動における体積移動で捉えると、慣性抵抗が実質と機能の釣り合いを示すことが容易に理解できる(図）。

地球と月は二つで一つの系を成す？

ここで序文の地球と月の関係に戻り考えてみる。ニュートンの万有引力の概念には相対的視点が欠けていた。コペルニクス的転換で天動説は地動説に変わったが、マッハの相対論に倣えば、そのどちらでもなく全体相対運動説が正しいように思える。
地球と月の関係は、地球を絶対中心に月が軌道周回する二者相互間だけの「閉じた運動系」の中で対立構造として捉えており、系内の力の釣り合いだけで考えられている。ニュートン力学が「絶対空間、絶対時間の静的宇宙像」に依拠していることからもそれは明らかである。(歴史的、宗教的背景が関与)
しかし全宇宙との相互的関係からみると、むしろ地球と月は一つの内系と合わせみなし、系内の力(内力)と系外の力（外力）の釣り合いと捉えるべきではないだろうか。
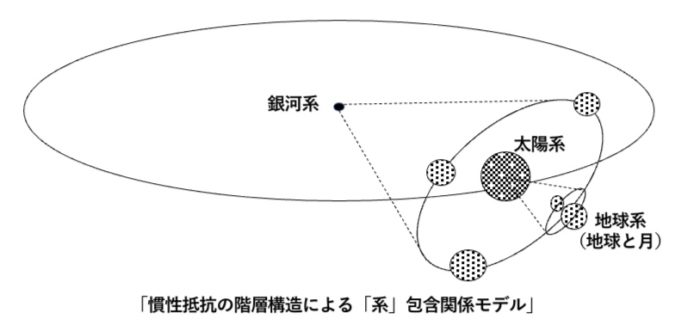
このようにみると、地球と月は一つとなり、まるで「我々の身体にみられる吊性置性のダブルコーンになっている」ようにみえてくる。地球が置性円錐、月が吊性円錐をなし、一つの系としての構造をもつと考えられるのである。

この考えに至り、改めて宇宙の階層構造は全て相似形を成すという不思議を感じた。地球と月の複合体と我々の身体は幾何学的相似形にみえる。人体吊性円錐の焦点も太陽系の重心へ収束し、そこから連綿と宇宙全体に包含され、地球の重力が成す置性円錐と釣り合っているのではないだろか。（図）

そもそもニュートン「力学」が「力」という概念を持ち込んだことから現在も「4つの相互力」として学問的慣習的に使用されていることが問題に思え、構造医学の原理にも執筆当時の学問慣習に倣い相互力と記されているが、相互作用とするのが正しいことが以前から構造医学講義で説かれている。

すると万有引力とは全く異なる解釈となり、月が地球に落下してこないのは、地球の重力に負けないように月が運動して釣り合っているのではなく、地球と月は二つで一つの系であり、地球の重力と月の質量および運動量(地球の重力による落下運動)に対する系外からの慣性抵抗、即ち地球の重力質量と月の慣性質量との釣り合いで月は落ちてこないし、地球は太陽系との釣り合いを保てると考えられないだろうか。

そもそも重力は対数螺旋渦であり、対数螺旋の性質は中心に近づくにつれ指数関数的、角加速度的に速度増大するのであり、角加速度に釣り合うのは角加速度だけなのだから、重力＝加速度は成立せず、重力に釣り合うのは同じく角加速度を示す重力だけであるはずである。
それは自然界に見られる渦運動にも流体力学的に示されており、渦には「自然渦」と洗濯機の渦のような外力による「強制渦」の二種類があるが、自然界に見られる渦が自然渦だけで成立することはないとされる。なぜなら地球の重力がつくりだす自然渦だけなら、前述したように、渦の中心速度は無限大に発散してしまうことになるため、必ず外側に強制渦が生じて釣り合いをとる。(ランキン渦と呼ばれる)
この外周軌道の強制渦をつくるのは、渦の運動系外の慣性抵抗と考えられ、つまりこれも地球の重力と全宇宙の慣性抵抗の釣り合いがつくりだす意味において、洗濯機の強制渦とは異なる自然渦であり、自然の運動全てに働く動的な釣り合いの原理と考える。大学研究機関等で渦発生装置を用いて銀河運動を解析する試みがなされているが、人工的につくりだす渦運動では本態は解けないように思える。
これは運動の相似性だけでなく、形の相似性にも現れ、自然に現れるフラクタル形状(海岸線の形や生物の血管分岐や腸壁など)は全て自己相似形であり、極限まで小さな単位で計測しようとすると逆に距離は無限大に発散することから、形の自己相似形が無限の階層的連続性をもつことが示されている。

非対称性と対称性の幾何学思想

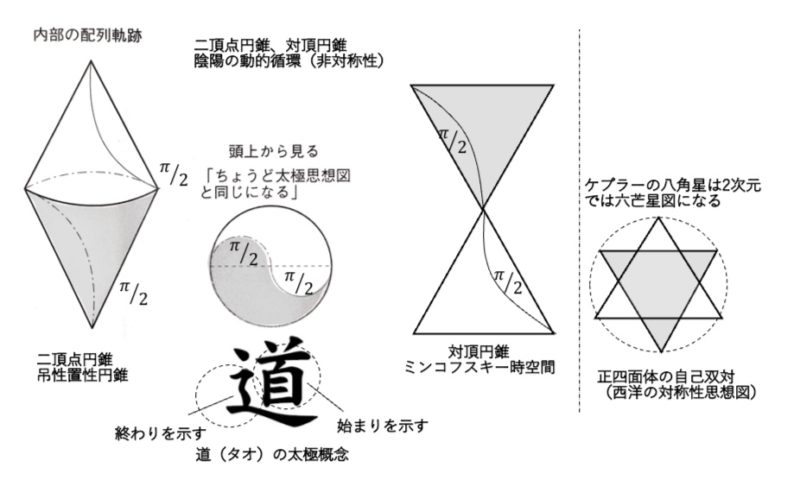
吊性系と置性系の重なる円錐は構造医学の理念をシンボル化した幾何学であるが、講義でもあるように、これを上下の収束点からπ/2の軌道螺旋を描き、軸方向から平面に捉えると太極図となる(図)。

太極図は無と有、陰陽すべてを非対称性の動的な螺旋渦の流れに包含する重力そのものを表現されている。
対して西洋は対称性を指向するのであり、これは立体だと正四面体自己双対多面体であるケプラー八角星などに表され、平面にすると「ダビデの星（六芒星）」となる。以前に学会発表でも触れたが、筆者にはWB構造がケプラーの八角星の対称性構造をもつようにみえる。（図） この対称性の高い構造が完全であるなら動きは生じないのであり、ほんの少しだけ対称性を破る、すなわち僅かな非加重側を潜在的に生じるから一歩目が踏み出せるということも宇宙の構造同様である。全ての事象は西洋的対称性と東洋的非対称性が相補的に作用しているようである。

つづきは後日掲載します。

---

参考引用文献

構造医学の原理　吉田勧持　エンタプライズ
構造医学の臨床　吉田勧持　エンタプライズ
構造医学解析I　吉田勧持　エンタプライズ
構造医学　自然治癒の鍵は重力にある！　吉田勧持　エンタプライズ
「歩行」と「脳」吉田勧持　エンタプライズ
男女対照　生体の構造とデザイン　アレグザンダー・シアラス　邦訳監修　吉田勧持　
医学概論　第一部　科学について　澤瀉久敬　誠信書房
アンリ・ベルクソン　澤瀉久敬　中公文庫
意識に直接与えられたものについての試論　アンリ・ベルクソン　ちくま学芸文庫
創造的進化　アンリ・ベルクソン　ちくま学芸文庫
物質と記憶　アンリ・ベルクソン　講談社学術文庫
思考と動き　アンリ・ベルクソン　平凡社ライブラリー
流れとかたち　エイドリアン・ベジャン&J・ペダー・ゼイン　紀伊國屋書店
対称性　レオン・レーダーマン 白揚社
カオスの自然学　テオドール・シュベング　工作舎
時間と空間　エルンスト・マッハ　法政大学出版局
哲学と宗教全史　出口治明　ダイヤモンド社
生物のかたち　ダーシー・トムソン　UP選書
野生の思考　クロード・レビィ=ストロース　みすず書房
構造主義　ジャン・ピアジェ　白水社
構造主義生物学 柴谷篤弘 東京大学出版会
構造主義方法論文入門　高田明典　夏目書房
構造主義進化論入門　池田清彦　講談社
エピジェネティックス　仲野徹　岩波新書
宇宙船地球号　バックミンスター・フラー　ちくま学芸文庫
かたち〜自然が創り出す美しいパターン　F・ボール　早川書房
図解　縄文大爆発　大谷幸市　parade books
第21回日本構造医学会論文集「要素比較人類学的考察」原口誠
第23回日本構造医学会論文集「置性系、吊性系の平衡メカニズムの考察」原口誠
「絵画協力」タイトル「ミクロコスモス」吉村ゆり