「生理反応重力場の理論」についての試論 ～Vol.２～

構造(関係)論からの宇宙創生論

宇宙論諸説百花繚乱の昨今、それらの理論を一通りみていくと、興味深い理論が多くあるものの全ては仮説であり、結局はそれらの仮説を証明するための物質同定(重力子のような)や観測データを得ることに偏っている気がする。
筆者も宇宙や重力について調べ学ぶ過程で、複雑な理論に翻弄され、囚われてしまいそうになることを実感し、このように既に現存する事象を、要素還元論的に分析していくだけでは宇宙や重力の本質と生物の関わりは見えてこないように思われ、事象の成り立ちから構造関係論的にシンプルに全体像を捉える目線が必要な気がした。そのヒントは、構造医学の原理　第一章「容器反応系」の概念にあると考える。重要な一文を要約すると「創造のための第一歩は人体のモデル化であり、一般的モデルは機能中心的性状モデルで内容物要素の究明に偏っており、構造医学は外形つまり「器とそれに馴染む内容物との関わり」を総合的にみつめ、全体的「態」の推移変換に着目し容器反応系モデルを導入する」とある。
これを医療者目線で捉えると人体の話だけのように狭視野的に捉えてしまいがちだが、ここでは宇宙の構造から人体構造を演繹しているのであり、ならば容器反応系モデルとは宇宙構造全体もそのようにできていると捉えるべきだと気づいた。
よって筆者もそれに倣い、容器反応系モデルを柱に、太極的視座から構造論的に宇宙の構造を考えてみた。

「容器反応系として捉える宇宙構造」
　観測、実証技術を持たなかった時代の物理学は、自然現象そのものの観察を重視し、仮説モデルを演繹的に構築する手法がとられていたが、現代物理学は実証科学的な色合いが濃くなっているように感じる。
高度な数学を駆使するため、一見すると数学に近い学問に思えるが、現代数学が量的計算や数や形など要素(内容)の性質一切を捨象し、要素を変換する操作とそれが成す関係性(構造、外形)を重視するのに対して、物理学はその性質上、「量(単位、計測)」という問題を扱うため、その基本的性質はどうしても要素還元論的立場も取らざるを得ず、特に現代の実証科学的物理学は数学とは根本的には対照的学問性質にあるようだ。

ここで、そもそも計量とは何か考える必要がある。その前に構造の考え方について触れると、構造(関係)論的に事物を捉える思考体系が構造主義であり、ソシュール言語論を祖とし、社会人類学者のレビィ=ストロースが応用学へ発展させたとされるが、さらに起源を辿ると東洋の道家(道教)、太極思想や仏教にまで遡る。大乗仏教中観派の祖、ナーガルジュナの説いた空論は、「諸法は無自性であり、空である」とし、全ての事物は「相依性」であると説く。「空」の意味は誤解されがちだが、その概念は虚無的な意味とは真逆の、「事象全ての状態確率を包含する選択場、言い換えれば無限大のポテンシャルを秘めた場」のような状態を意味する。般若心経の「色即是空　空即是色」にも空論は反映されている。太極思想も基本的に同じであり、太極図は事象の相対性的本質を見事に表現している。(これらが量子力学の世界観と驚くほど似ていることは多くの量子物理学者も認めることである。)
この意味において、「無」の存在すらアプリオリに定義できないのであり、「無」や「有」という言葉と概念自体、人間が一つの全体を恣意的に切り分け名前と概念を与えなければ何も語れないというソシュール言語構造主義の指摘が見事に当てはまっている。

計量も全く同じ構造であり、「本来不可分な自然を空間的距離や時間や長さ、重さという人間の尺度で恣意的に分割し、単位づけたもの」であり、その物差しを使って自然を理解しようとするのが物理学といえる。
言語、計量ともに人類に欠かせない大発明なのだが、これらの問題は、分割した事物に名前や単位を与え概念化した時から、それがいつしか固有に存在する絶対的、先天的に実在するものであるかのような固定観念に囚われ、事物の本質をありのままに観る目を眩ましてしまうことにある。
固定観念を取り払い、ありのままに観るには、「名前や単位といったあらゆる概念を捨て」、自然現象を捉え直す必要がある。もし名前や計量概念が無かったら、我々は自然をどう観るのか、物心つく前の子供や原始の人類目線で考えてみる。そこで一番重要な概念は時間である。原始の計量概念の発露は全て時間に包含されると考えられるからである。
時計もなく時間の概念すらなければ、それは「態の変化」として認識されるだけである。態の変化は動き、流れと同義であり、外界の自然の態の推移変化と、それを感じている自己の意識の流れ、変化をただ感じるだけのはずである。

空間の距離はどうか。それも移動するという態の変化によって最初に認識され、移動による外界の景色の変化をただ認識するだけだろうし、温度は熱かったものが冷めていく変化を認識することで知る。重さは立っている自己の体重を感じ、物を持った際の重さの変化を感じ、自ら動く際や物を動かそうとする際に感じる抵抗として認識される。つまり全ては外界環境と内界の意識の持続的な態の推移変化をありのままに認識されるだけの世界となる。
ここから逆に考えると、全ての量的計量的概念は時間的な態の推移変化としてしか捉えることができないことがわかる。では態の変化は何により起こるのか。それを一つの言葉で表すならエネルギーの変化と流れとなる。ではなぜエネルギーは流れるのか、エネルギーとは何か。宇宙を一つの容器に例えるなら、それは容器の内容である。ではその容器とは何か、エネルギーを包含する空間の構造だろう。

ならば空間が幾何学的対称構造であればどうなるか、動き、流れ、即ち時間は生じない。つまり容器である空間構造そのものの対称性が破れていなければならない。その空間構造の対称性を破る形は「螺旋」であり、その螺旋を形づくるものこそが「重力」だと考えれば納得できる。相対性理論によれば重力とは時空間構造の歪みそのものだからである。
つまり宇宙の構造や重力の本質は、トポロジー(位相空間論)的問題である可能性があり、重力が位相空間構造そのものをつくる容器の一部のような存在であれば、重力を内容物として理解しようとする試みは問題の出発点がずれていることになり、器を内容と捉え、物質同定しようとする目線である限り、四つの相互作用は統一できないのではないだろうか。全ての物理現象は「場」を与えなければ議論できないが、場とは即ち容器であり、なんらかの場をもとに考える理論が、場の存在そのものを問うことはできないように思えるのである。
この容器と内容の相互関係として宇宙を捉えるとどう解釈できるのか。位相空間論的には宇宙は多次元構造であることが推測されているが、難しく考えずに重力の幾何学形状である円錐として捉え考えてみる。

学問上の慣習に倣えば、まずビッグバン(始まりの特異点)があった。インフレーションによるエネルギーと空間の指数関数的膨張は円錐の発散方向へ拡がり、同時に円錐の特異点に収束する重力も発生する。
これらは同時に相依性に成立しなければ、一瞬で発散か収束して終わりとなることがわかり、宇宙が現存するのは、現在も発散と収束が同時的に釣り合っているからと考えられる。その証拠として宇宙は光速度で現在も膨張を続けているとされ、対する重力の伝達速度も同じく光速度で釣り合っていると考えられるからだ。そこで前章で触れた、E=mc²の光速度累乗の意味を物理科学理論的複雑に考えるのではなく構造関係からシンプルに考えると、「発散(動)と収束(静)の双極へ光速度で向かう宇宙の相互作用の釣り合いのポテンシャルエネルギーから物質が生まれた」と考えられないだろうか。（図）

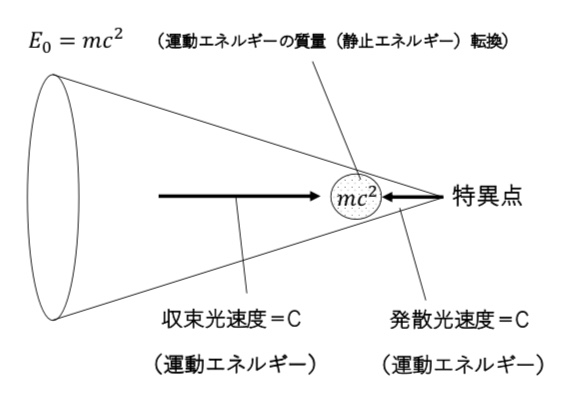
原初のエネルギーが質量0の光エネルギーのようなものだったとする。点から拡散方向へ拡がる光の動的性質に対し、重力は点に収束する静的性質をもつ。
これらが一点で相互作用すればどうなるか、それを考えるには「粒子と反粒子の対生成と対消滅」のモデルを考えれば理解しやすい。

対消滅では、粒子と反粒子の衝突による「質量欠損」において、質量エネルギーは「静止エネルギー」とそれらが持っていた運動エネルギーの和に相当するエネルギーがγ線のような強い光エネルギーに変換される。核分裂により質量のほんの一部を喪失するだけで凄まじいエネルギーを発する原子爆弾から類推すれば、全質量喪失のエネルギー変換は桁違いのエネルギーを生み出すことがわかる。

一方、対生成では粒子と反粒子の衝突融合はそれらの運動エネルギー全てが静止エネルギーに変換され、それは反発する二つを融合するだけの莫大な「束縛エネルギー」に等しい。
E=mc²が物質質量の存在そのものがもつ静止エネルギーを示すと考えれば、「物質とは運動エネルギーを静止することで生じるもの」と考えることが本質的である。つまり原初の質量をもたない強力な光エネルギーが、特異的収束密度の中で衝突し、静止エネルギーを得ることで質量をもつ粒子が生じたと考えれば良いのではないか。そして質量をもつ粒子と反粒子が対生成と対消滅を繰り返しながら電荷の反発する陽子と電子を束縛する静止エネルギー相当の核力(強い相互作用力)が生じ、原子が生成されたと考えれば、質量や物質とは前述したように「運動エネルギーの静止エネルギー（物質の重力質量）転換」と定義できるのではないだろうか。このように考えれば、「質量とエネルギーの等価式」にc²が含まれる意味が理解できそうな気がする。

すると重力とは、時空間の対称性を破り、動きを創生する存在であると同時に、全ての動き、換言すれば時間を止める、または遅らせる全能の存在のようであり、極論すれば「時間とは重力の機能の一部」とも考えられ、その時間と空間が結びついた時空間という容器そのものであるとあらためて思えてくる。
この解釈から重力質量と慣性質量を考えれば、完全に静止状態にある時、それは物質の置かれた「態」として静止エネルギーがそのまま重力質量で表現され、運動の「態」にある時、重力はそれらの時間を静止する方向に作用するため、運動を遅らせる抵抗力即ち慣性力(抵抗)として表現されるとも解釈できる。つまり重力の本質とは「力」ではなく、「時間的作用」と捉えるべきなのではないのか。体組成の99%が水であるクラゲの運動に自身の鏡像の如き水流虚像をみるとき、実時間と反転した虚数的時間(過去)との時間対称性の現れのように思えるのである。（図）

次に、この解釈をもとに重力と生物の関わりを捉えてみる。熱力学のエントロピー増大則で考えると、宇宙は発散と収束の釣り合いをとりつつも膨張傾向への趨勢をもつことから、僅かながらこの釣り合いの対称性を欠いていると考えられ、よって物質の時間的「態」の推移は必ず崩壊拡散へ向かう。そこで無生物の物質をみると、その「態」は静止であり、重力質量としてただそこに存在している。この重力質量に変化はないので、エントロピーに従い拡散へ向かうことは「決定的」である。
一方の生物、特に動物は動くものである。「不断の動き」は重力質量から慣性質量へ変化し、その移動速度によって「慣性抵抗としての重力は僅かに増加」する。重力の抵抗を受けるとは、無秩序（カオス系）を束縛収束し構造的秩序をもたらすことに他ならず、「生物の能動性」とはエントロピーの決定性に従わない「非決定的要素」を重力により取り込む姿ととらえられ、それは即ち全ての物質に働くエントロピーの時間進行をも遅らせることと考えられるのである。このように容器反応系とは内外の物質やエネルギーのやり取りのみならず、常に「態」を変化させることにより、対称性や決定性を破ることで外界と共存する系としてとらえることができる。
(宇宙の対称化は熱的平衡。物質や生物の存在は宇宙からみれば対称性を破る存在。物質や生物側からみれば、全体平衡化とは無秩序であり、構造を保つ作用(重力)が秩序を与えるという対立構造になっている。無秩序の中で、本来結びつかないものを結びつけることを吉田勧持先生は「カオスの系（カオス連絡）」という言葉で説明されている。季刊構造医学通巻第8号)

つづきは後日掲載します。

---

参考引用文献

構造医学の原理　吉田勧持　エンタプライズ
構造医学の臨床　吉田勧持　エンタプライズ
構造医学解析I　吉田勧持　エンタプライズ
構造医学　自然治癒の鍵は重力にある！　吉田勧持　エンタプライズ
「歩行」と「脳」吉田勧持　エンタプライズ
男女対照　生体の構造とデザイン　アレグザンダー・シアラス　邦訳監修　吉田勧持　
医学概論　第一部　科学について　澤瀉久敬　誠信書房
アンリ・ベルクソン　澤瀉久敬　中公文庫
意識に直接与えられたものについての試論　アンリ・ベルクソン　ちくま学芸文庫
創造的進化　アンリ・ベルクソン　ちくま学芸文庫
物質と記憶　アンリ・ベルクソン　講談社学術文庫
思考と動き　アンリ・ベルクソン　平凡社ライブラリー
流れとかたち　エイドリアン・ベジャン&J・ペダー・ゼイン　紀伊國屋書店
対称性　レオン・レーダーマン 白揚社
カオスの自然学　テオドール・シュベング　工作舎
時間と空間　エルンスト・マッハ　法政大学出版局
哲学と宗教全史　出口治明　ダイヤモンド社
生物のかたち　ダーシー・トムソン　UP選書
野生の思考　クロード・レビィ=ストロース　みすず書房
構造主義　ジャン・ピアジェ　白水社
構造主義生物学 柴谷篤弘 東京大学出版会
構造主義方法論文入門　高田明典　夏目書房
構造主義進化論入門　池田清彦　講談社
エピジェネティックス　仲野徹　岩波新書
宇宙船地球号　バックミンスター・フラー　ちくま学芸文庫
かたち〜自然が創り出す美しいパターン　F・ボール　早川書房
図解　縄文大爆発　大谷幸市　parade books
第21回日本構造医学会論文集「要素比較人類学的考察」原口誠
第23回日本構造医学会論文集「置性系、吊性系の平衡メカニズムの考察」原口誠
「絵画協力」タイトル「ミクロコスモス」吉村ゆり