「生理反応重力場の理論」についての試論 ～Vol.１～

はじめに

「お月様はなぜお空に浮いているの？」。

　子供時代は誰もが不思議に思えたはずである。「地球の引力と月の遠心力という力が釣り合って…云々」と説明できる大人もいるだろうが、物理学的に解明されているのだからそういうものだろうと無批判に思いこんでいる大人が大多数だろう。見たこともない宇宙の話ならいざ知らず、「水はなんで下へ流れるの？」という日常的な現象の質問にも「重力の働きだよ」と答えるのだが重力とは何か？概念は知っていても本当のところは大人だって知らない。

前述した月の説明も同じで、学校では遠心力(慣性力)は「見かけの力」と教わるのだが、見かけの力で月が浮いているという説明で子供は納得するだろうか。遠い宇宙の話ならいざ知らず、日々体感している遠心力が見かけの力だと子供に納得させるのはかなり難しいだろう。しかし学校に通い始め、型枠的教育に嵌められていく過程で、一つの疑問に拘っている時間もなく、教科書に書いてあるニュートンの運動方程式を覚え、慣性力は見かけの力と書いてあればそれは当然正しいものと受け入れ、そのように回答すれば正解がもらえるのだから、例えそれが自分の体験や感覚に反するものでも「科学的事実」とされれば無批判に受け入れる習慣がつき、我々は大人になる。

しかし全ての科学の基礎となる物理学、それも重力の理解さえ見かけの力という曖昧、未明な解釈問題を残した上に築かれているならば、科学に依拠する全ての学問が科学的事実、根拠に基づくなどと簡単にはいえないことになり、それは医学とて例外ではない。ましてや「生理重力」を診療指針にする我々にとってそれは自明なものとして看過できる問題ではなく、一度は重力にとことんまで向き合って「自分自身で」考える必要があると考えた。 サン=テグジュペリ作「星の王子さま」の「本当に大切なものはみえない、大人にはみえない」という下りがあるが、それは概念理解で事物を知った気になり、自然をありのままに観て素朴な疑問をもてなくなる大人達の問題を暗喩しているのではないだろうか。

ピアジェの思考発達段階説では、2歳くらいまでの感覚運動段階期は、感覚と運動が表象(言語、記号)を介さずに直接結び付いている時期とされ、以後擬人的な理解から具体、抽象思考へと発達するとされるが、これは個人の成長過程のみならず人類の思考発達段階をも表しており、ありのままに観るとは2歳児以前の感覚運動段階に還り事物を捉えることと考える。

本稿は「構造医学の原理　自序及び第一章」について、その意味せんとすることを独自に解釈し、とりまとめた試論である。第一章には星の王子さまと同じような問題提起が暗喩されているように感じる。構造医学を学び始め20年数年経った現在、過去の反省を総括する意味で、科学的な知見は重視しながらも、「事物をできるだけありのままに観る」態度でこの難題に取り組んでみた。

重力について

序文の月の疑問に現在の常識概念で答えるなら、「地球の万有引力と、月の慣性力(遠心力+コリオリ力)の釣り合い」で説明されるわけだが、問題は「慣性力=見かけの力」とはどのような論理から導かれたのか、この辺りを考えることが重力本質理解の鍵となりそうである。

構造医学における重力の捉え方の基本をまず整理すると、引力とは斥力であり、重力の本質である積層力とは似て非なるものとし、慣性質量と重力質量を、重力の機能(吊性系)と実質構造(置性系)という概念に置き換えて説明される。
構造医学では慣性力は見かけの力などではなく、とくに吊性運動時の機構平衡器の慣性制御に関わる「機能」として重要視するのであるが、物理や工学の専門家達の間でも未だ慣性力については所説様々で統一見解はなく(慣性系の引きずり説が有力視される)、ニュートン力学の説明通り教科書でも依然「見かけの力」と教えられているようである。

そもそもニュートン「力学」が「力」という概念を持ち込んだことから現在も「4つの相互力」として学問的慣習的に使用されていることが問題に思え、構造医学の原理にも執筆当時の学問慣習に倣い相互力と記されているが、相互作用とするのが正しいことが以前から構造医学講義で説かれている。

慣性力が見かけの力であることは、ダランベールの原理に依拠しているとされ、それは以下のようなものだ。

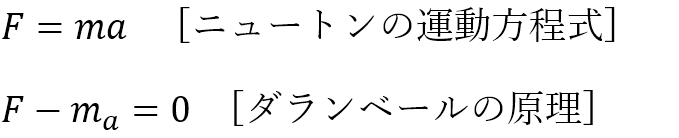
上記のように運動方程式を置き換え、関係性が明示化される。この式だけみると、確かに数式上、また「力」を実体的なものと捉えれば、は見かけの力とみえなくもない。運動の第三法則(作用反作用の法則)的に釣り合う力がないこともわかる。

ただ、この式から慣性力を見かけの力と解釈するには、静的平衡状態として解釈した時だけのようにも思え、動的平衡の視点からは異なる解釈もできるのではないだろうか。ようするに加速度運動する際の加速度に対する物体からの機能的応答が相対加速度の慣性抵抗であり、動的平衡状態を表現しているとも解釈できるのであり、むしろ慣性抵抗を日々体感している普通の感性で捉えればそう解釈した方が自然に思えるのだが、惑星間の運動を説明する上で引力的な力の釣り合いを前提に考えれば、力を実体的に捉える立場からは、向心力に対する慣習力が見かけの力であってくれないと整合性がとれなかったことのではないだろうか。(慣性力という表現が問題だと思うので、以後筆者の意見として使用する際は慣性抵抗と記す。）

さらにニュートンの運動方程式を慣性質量と見做し、等価原理に適用されたことにより、

以後、重力は相対性理論により「場の理論」として捉えられるようになり、重力場という時空間構造の歪みが重力の正体であることが明らかになる。

アインシュタインの「質量とエネルギーの等価性」を示す式「E=mc²」には重力の本質理解の鍵が隠れているように思える。
E=mc²の式をみる時、その名の示すようにエネルギーと質量の関係にだけ目が囚われてしまうが、重要なのはむしろc²(光速度の累乗) をどう解釈するかではないだろうか。この式の本質的重要性は、「質量が生まれる原理」を明らかにしたことだと考える。
E=mc²のm項を極限に小さくとれば、c²が残る。光は現在のところ質量0とされ、ゆえに宇宙最速である。重力の伝達速度も光速度で伝達することは証明されており、質量を持つ物質は光速度を超えることはできない。この条件をもとに、難しい数学抜きに構造関係論的にこの式の意味を捉えればどう解釈できるか、次章で考えてみる。

つづきは後日掲載します。